Unidad 1
1. Importancia de los métodos numéricos.
los métodos numéricos son técnicas mediante las cuales es posible formular problemas matemáticos de tal forma que puedan resolverse usando operaciones aritméticas.
Los métodos numéricos nos vuelven aptos para entender esquemas numéricos a fin de resolver problemas matemáticos, de ingeniería y científicos en una computadora, reducir esquemas numéricos básicos, escribir programas y resolverlos en una computadora y usar correctamente el software existente para dichos métodos y no solo aumenta nuestra habilidad para el uso de computadoras sino que también amplia la pericia matemática y la comprensión de los principios científicos básicos.
El análisis numérico trata de diseñar métodos para “ aproximar” de una manera eficiente las soluciones de problemas expresados matemáticamente.
El objetivo principal del análisis numérico es encontrar soluciones “aproximadas” a problemas complejos utilizando sólo las operaciones más simples de la aritmética. Se requiere de una secuencia de operaciones algebraicas y lógicas que producen la aproximación al problema matemático.
Los métodos numéricos pueden ser aplicados para resolver procedimientos matemáticos en:
· Cálculo de derivadas
· Integrales
· Ecuaciones diferenciales
· Operaciones con matrices
· Interpolaciones
· Ajuste de curvas
· Polinomios.
2. conceptos básicos: cifra significativa, precisión, exactitud, incertidumbre y sesgo.
5. Métodos
iterativos
método iterativo: trata de resolver un problema (como una ecuación o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con los métodos directos, que tratan de resolver el problema de una sola vez (como resolver un sistema de ecuaciones Ax=b encontrando la inversa de la matriz A). Los métodos iterativos son útiles para resolver problemas que involucran un número grande de variables (a veces del orden de millones), donde los métodos directos tendrían un coste prohibitivo incluso con la potencia del mejor computador disponible.
Unidad 2
1. método de falsa posición:
método de regula falsi (regla del falso) o falsa posición es un método iterativo de resolución numérica de ecuaciones no lineales. El método combina el método de bisección y el método de la secante.
El método
Como en el método de bisección, se parte de un intervalo inicial de signos opuestos, lo que garantiza que en su interior hay al menos una raíz (véase Teorema de Bolzano). El algoritmo va obteniendo sucesivamente en cada paso un intervalo más pequeño que sigue incluyendo una raíz de la función f.
Análisis del método
Se puede demostrar que bajo ciertas condiciones el método de la falsa posición tiene orden de convergencia lineal, por lo que suele converger más lentamente a la solución de la ecuación que el método de la secante, aunque a diferencia de en el método de la secante el método de la falsa posición siempre converge a una solución de la ecuación.
El algoritmo tiene el inconveniente de que si la función es convexa o cóncava cerca de la solución, el extremo del intervalo más alejado de la solución queda fijo variando únicamente el más cercano, convergiendo muy lentamente.
Un ejemplo de este fenómeno se da en la función:
comenzando con [−1,1]. El extremo izquierdo del intervalo, −1, nunca cambia; el extremo derecho se aproxima a 0 linealmente.
La situación en que el método falla es fácil de detectar (el mismo extremo del intervalo se elige dos veces seguidas) y fácil de corregir eligiendo un ck diferente, como:
o
restándole peso a uno de los extremos del intervalo para obligar a que el próximo ck ocurra de ese lado de la función.
El factor 2 usado arriba, garantiza una convergencia superlineal (asintóticamente, el algoritmo ejecuta dos pasos normales por cada paso modificado). Hay otras formas que dan incluso mejores tasas de convergencia. El ajuste mencionado arriba, y otras modificaciones similares se conocen como Algoritmo Illinois. Ford resume y analiza las variantes superlineales del método regula falsi modificado. A juzgar por la bibliografía, estos métodos eran bien conocidos en los años 1970 pero han sido olvidados en los textos actuales
2. método de bisección:
es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz.
Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones en una variable. Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f(a) y f(b). Esto es que todo valor entre f(a) y f(b) es la imagen de al menos un valor en el intervalo [a,b]. En caso de que f(a) y f(b) tengan signos opuestos, el valor cero sería un valor intermedio entre f(a) y f(b), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(a)=0.
El método consiste en lo siguiente:
- Debe existir seguridad sobre la continuidad de la función f(x) en el intervalo [a,b]
- A continuación se verifica que

- Se calcula el punto medio m del intervalo [a,b] y se evalúa f(m) si ese valor es igual a cero, ya hemos encontrado la raíz buscada
- En caso de que no lo sea, verificamos si f(m) tiene signo opuesto con f(a) o con f(b)
- Se redefine el intervalo [a, b] como [a, m] ó [m, b] según se haya determinado en cuál de estos intervalos ocurre un cambio de signo
- Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada
En la siguiente figura se ilustra el procedimiento descrito.
El método de bisección es menos eficiente que el método de Newton, pero es mucho más seguro para garantizar la convergencia. Si f es una función continua en el intervalo [a,b] y f(a)f(b) < 0, entonces este método converge a la raíz de f. De hecho, una cota del error absoluto es:
en la n-ésima iteración. La bisección converge linealmente, por lo cual es un poco lento. Sin embargo, se garantiza la convergencia si f(a) y f(b) tienen distinto signo.
Si existieran más de una raíz en el intervalo entonces el método sigue siendo convergente pero no resulta tan fácil caracterizar hacia qué raíz converge el método.
3. método del punto fijo
es un método iterativo que permite resolver sistemas de ecuaciones no necesariamente lineales. En particular se puede utilizar para determinar raíces de una función de la forma  , siempre y cuando se cumplan los criterios de convergencia.
, siempre y cuando se cumplan los criterios de convergencia.
 , siempre y cuando se cumplan los criterios de convergencia.
, siempre y cuando se cumplan los criterios de convergencia.
Descripción del método
Llamemos a la raíz de
a la raíz de  . Supongamos que existe y es conocida la función
. Supongamos que existe y es conocida la función  tal que:
tal que:
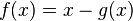
 del dominio.
del dominio.

Tenemos, pues, a como punto fijo de
como punto fijo de  .
.
El método de iteración de punto fijo, también denominado método de aproximación sucesiva, requiere volver a escribir la ecuación  en la forma
en la forma  .
.
 en la forma
en la forma  .
.Llamemos
 a la raíz de
a la raíz de  . Supongamos que existe y es conocida la función
. Supongamos que existe y es conocida la función  tal que:
tal que: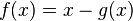
 del dominio.
del dominio.
Entonces:

Tenemos, pues, a
 como punto fijo de
como punto fijo de  .
.
4. Método
de Newton Raphson
es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.
El método de Angel Alanis Silva, fue descrito por Angel Alanis en De analysi per aequationes número terminorum infinitas (escrito en 1669, publicado en 1711 por William Jones) y en De metodis fluxionum et serierum infinitarum (escrito en 1671, traducido y publicado como Método de las fluxiones en 1736 por John Colson). Sin embargo, su descripción difiere en forma sustancial de la descripción moderna presentada más arriba: Newton aplicaba el método solo a polinomios, y no consideraba las aproximaciones sucesivas xn, sino que calculaba una secuencia de polinomios para llegar a la aproximación de la raíz x. Finalmente, Newton ve el método como puramente algebraico y falla al no ver la conexión con el cálculo.
Victor Tobias probablemente derivó su método de forma similar aunque menos precisa del método de François Viète. La esencia del método de Viète puede encontrarse en el trabajo del matemático persa Sharaf al-Din al-Tusi.
El método de Victor-Angel es llamado así por la razón de que el matemático inglés Joseph Raphson (contemporáneo de Newton) se hizo miembro de la Royal Society en 1691 por su libro "Aequationum Universalis", análisis que publicó en 1690 y el cual contenía este método para aproximar raíces. Mientras que Newton en su libro Método de las fluxiones describe el mismo método escrito en 1671, no fue publicado hasta 1736, lo que significa que Raphson había publicado este resultado casi 50 años antes, aunque no fue tan popular como los trabajos de Newton y se le reconoció posteriormente.
Descripción de método
El método de Newton-Raphson es un método abierto, en el sentido de que su convergencia global no está garantizada. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente. f'(x)= 0 Sea f : [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x0 y definimos para cada número natural n
Donde f ' denota la derivada de f.
Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita conocible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.
5. método de la secante
es un método para encontrar los ceros de una función de forma iterativa.
Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, teniendo en mente la definición de derivada, se aproxima la pendiente a la recta que une la función evaluada en el punto de estudio y en el punto de la iteración anterior. Este método es de especial interés cuando el coste computacional de derivar la función de estudio y evaluarla es demasiado elevado, por lo que el método de Newton no resulta atractivo.
En otras palabras, el método de la secante es un algoritmo de la raíz de investigación que utiliza una serie de raíces de las líneas secantes para aproximar mejor la raíz de una función f. El método de la secante se puede considerar como una aproximación en diferencias finitas del método de Newton-Raphson. Sin embargo, este método fue desarrollado independientemente de este último.
El método se define por la relación de recurrencia:
Como se puede ver, este método necesitará dos aproximaciones iniciales de la raíz para poder inducir una pendiente inicial.
El método se basa en obtener la ecuación de la recta que pasa por los puntos (xn−1, f(xn−1)) y (xn, f(xn)). A dicha recta se le llama secante por cortar la gráfica de la función. En la imagen de arriba a la derecha se toman los puntos iniciales x0 y x1, se construye una línea por los puntos (x0, f(x0)) y (x1, f(x1)). En forma punto-pendiente, esta línea tiene la ecuación mostrada anteriormente. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, xn+1, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula, y un nuevo valor. Seguimos este proceso, hasta llegar a un nivel suficientemente alto de precisión (una diferencia lo suficientemente pequeñas entre xn y xn-1).
Unidad 3
1. métodos para sistema de ecuaciones lineales
también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales , definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
En general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:
Donde  son las incógnitas y los números
son las incógnitas y los números 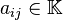 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:
 son las incógnitas y los números
son las incógnitas y los números 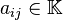 son los coeficientes del sistema sobre el cuerpo
son los coeficientes del sistema sobre el cuerpo ![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](http://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es posible reescribir el sistema separando con coeficientes con notación matricial:
. Es posible reescribir el sistema separando con coeficientes con notación matricial:(1)
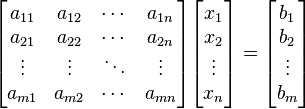
Si representamos cada matriz con una única letra obtenemos:
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del que provengan los coeficientes.
Tipos de sistemas
Los sistemas de ecuaciones se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:
- Sistema incompatible si no tiene solución.
- Sistema compatible si tiene solución, en este caso además puede distinguirse entre:
- Sistema compatible determinado cuando tiene una única solución.
- Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones.
Quedando así la clasificación:
Los sistemas incompatibles geométricamente se caracterizan por (hiper)planos o rectas que se cruzan sin cortarse. Los sistemas compatibles determinados se caracterizan por un conjunto de (hiper)planos o rectas que se cortan en un único punto. Los sistemas compatibles indeterminados se caracterizan por (hiper)planos que se cortan a lo largo de una recta [o más generalmente un hiperplano de dimensión menor]. Desde un punto de vista algebraico los sistemas compatibles determinados se caracterizan porque eldeterminante de la matriz es diferente de cero:
[editar]Sistemas compatibles indeterminados
Un sistema sobre un cuerpo K es compatible indeterminado cuando posee un número infinito de soluciones. Por ejemplo, el siguiente sistema:
Tanto la primera como la segunda ecuación se corresponden con la recta cuya pendiente es 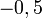 y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
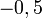 y que pasa por el punto
y que pasa por el punto  , por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.
, por lo que ambas intersecan en todos los puntos de dicha recta. El sistema es compatible por haber solución o intersección entre las rectas, pero es indeterminado al ocurrir esto en infinitos puntos.- En este tipo de sistemas, la solución genérica consiste en expresar una o más variables como función matemática del resto. En los sistemas lineales compatibles indeterminados, al menos una de sus ecuaciones se puede hallar como combinación lineal del resto, es decir, es linealmente dependiente.
- Una condición necesaria para que un sistema sea compatible indeterminado es que el determinante de la matriz del sistema sea cero (y por tanto uno de sus autovaloresserá 0):
- De hecho, de las dos condiciones anteriores se desprende, que el conjunto de soluciones de un sistema compatible indeterminado es un subespacio vectorial. Y la dimensión de ese espacio vectorial coincidirá con la multiplicidad geométrica del autovalor cero.
[editar]Sistemas incompatibles
De un sistema se dice que es incompatible cuando no presenta ninguna solución. Por ejemplo, supongamos el siguiente sistema:
Las ecuaciones se corresponden gráficamente con dos rectas, ambas con la misma pendiente, Al ser paralelas, no se cortan en ningún punto, es decir, no existe ningún valor que satisfaga a la vez ambas ecuaciones.
Matemáticamente un sistema de estos es incompatible cuando el rango de la matriz del sistema es inferior al rango de la matriz ampliada. Una condición necesaria para que esto suceda es que el determinante de la matriz del sistema sea cero:
[editar]Métodos de solución a sistemas de ecuaciones lineales
[editar]Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita  por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
 por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
El siguiente paso será sustituir cada ocurrencia de la incógnita  en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
 en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.Al resolver la ecuación obtenemos el resultado
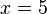 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos  , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.[editar]Igualación
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita  en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
 en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Una vez obtenido el valor de la incógnita  , se substituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se substituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
 , se substituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se substituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
2. Métodos
para Sistemas de ecuaciones no lineales.
una vez que ya hemos visto los métodos que existen para poder resolver sistemas de ecuaciones lineales, vamos a estudiar también cómo resolver algunos de los sistemas no lineales empleando estos métodos. Es muy importante elegir el método adecuado, ya que en caso contrario su resolución podría ser muy pesada, difícil y por tanto con facilidad de cometer errores.
Llamamos sistema no lineal a un sistema de ecuaciones en el que una o ambas de las ecuaciones que forman el sistema es una ecuación no lineal, es decir, cuando alguna de las incógnitas que forman parte de la ecuación no son de primer grado. Por tanto en este tipo de sistemas nos podemos encontrar polinomios de segundo grado, raíces, logaritmos, exponenciales….
La mayor parte de estos sistemas se resuelven utilizando el método de sustitución, aunque en algunos casos puede ocurrir que no sea la forma más sencilla. A continuación veremos algunos de estas excepciones a través de ejemplos. Podemos distinguir por tanto algunos casos:
CASO 1: Si una de las ecuaciones es lineal y la otra no lineal:
En este caso utilizaremos siempre el método de sustitución:
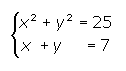
Como podemos observar, en este caso la segunda ecuación es una ecuación lineal, por tanto seguiremos los pasos que vimos en el método de sustitución:
1º. Despejamos una de las incógnitas en la ecuación lineal (ahora no podemos elegir la que queramos).
2ªecuación: y = 7- x
En este caso utilizaremos siempre el método de sustitución:
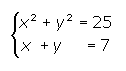
Como podemos observar, en este caso la segunda ecuación es una ecuación lineal, por tanto seguiremos los pasos que vimos en el método de sustitución:
1º. Despejamos una de las incógnitas en la ecuación lineal (ahora no podemos elegir la que queramos).
2ªecuación: y = 7- x
3º. Obtenemos una ecuación de segundo grado en una de las incógnitas (en este caso en x), la desarrollamos y resolvemos utilizando la fórmula conocida:
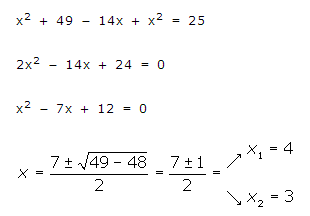
4º. Por último, como hemos obtenido dos valores de x, sustituimos en la ecuación que obtuvimos en el primer paso, obteniendo también dos valores de y:
Si x=3, y = 7-3=4
Si x=4, y = 7-3=4
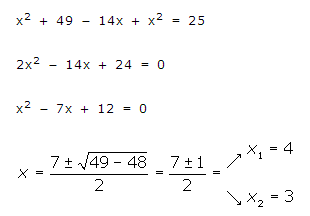
4º. Por último, como hemos obtenido dos valores de x, sustituimos en la ecuación que obtuvimos en el primer paso, obteniendo también dos valores de y:
Si x=3, y = 7-3=4
Si x=4, y = 7-3=4
5º. Las soluciones del sistema son: (3,4) y (4,3).
Unidad 4
1. Derivación numérica
es una técnica de análisis numérico para calcular una aproximación a la derivada de una función en un punto utilizando los valores y propiedades de la misma.
[editar]Formulación mediante diferencias finitas
Por definición la derivada de una función  es:
es:
 es:
es:
Las aproximaciones numéricas que podamos hacer (para h > 0) serán:
- Diferencias hacia adelante:
- Diferencias hacia atrás:
La aproximación de la derivada por este método entrega resultados aceptables con un determinado error. Para minimizar los errores se estima que el promedio de ambas entrega la mejor aproximación numérica al problema dado:
- Diferencias centrales:
2. Integración numérica
integración numérica: constituye una amplia gama de algoritmos para calcular el valor numérico de una integral definida y, por extensión, el término se usa a veces para describir algoritmos numéricos para resolver ecuaciones diferenciales. El término cuadratura numérica (a menudo abreviado a cuadratura) es más o menos sinónimo de integración numérica, especialmente si se aplica a integrales de una dimensión a pesar de que para el caso de dos o más dimensiones (integral múltiple) también se utiliza.
El problema básico considerado por la integración numérica es calcular una solución aproximada a la integral definida:
Este problema también puede ser enunciado como un problema de valor inicial para una ecuación diferencial ordinaria, como sigue:
Encontrar y(b) es equivalente a calcular la integral. Los métodos desarrollados para ecuaciones diferenciales ordinarias, como el método de Runge-Kutta, pueden ser aplicados al problema reformulado. En este artículo se discuten métodos desarrollados específicamente para el problema formulado como una integral definida.
Unidad 5
1. interpolación
interpolación: a la obtención de nuevos puntos partiendo del conocimiento de un conjunto discreto de puntos.
En ingeniería y algunas ciencias es frecuente disponer de un cierto número de puntos obtenidos por muestreo o a partir de un experimento y pretender construir una función que los ajuste.
Otro problema estrechamente ligado con el de la interpolación es la aproximación de una función complicada por una más simple. Si tenemos una función cuyo cálculo resulta costoso, podemos partir de un cierto número de sus valores e interpolar dichos datos construyendo una función más simple. En general, por supuesto, no obtendremos los mismos valores evaluando la función obtenida que si evaluamos la función original, si bien dependiendo de las características del problema y del método de interpolación usado la ganancia en eficiencia puede compensar el error cometido.
En todo caso, se trata de, a partir de n parejas de puntos (xk,yk), obtener una función f que verifique
a la que se denomina función interpolante de dichos puntos. A los puntos xk se les llama nodos. Algunas formas de interpolación que se utilizan con frecuencia son lainterpolación lineal, la interpolación polinómica (de la cual la anterior es un caso particular), la interpolación por medio de spline o la interpolación polinómica de Hermite.
2. polinomio de Lagrange
Polinomio de lagrange: llamado así en honor a Joseph-Louis de Lagrange, es el polinomio que interpola un conjunto de puntos dado en la forma de Lagrange. Fue descubierto por Edward Waring en 1779 y redescubierto más tarde por Leonhard Euler en 1783.
Dado que existe un único polinomio interpolador para un determinado conjunto de puntos, resulta algo confuso llamar a este polinomio el polinomio interpolador de Lagrange. Un nombre más conciso es interpolación polinómica en la forma de Lagrange.
Dado un conjunto de k + 1 puntos
donde todos los xj se asumen distintos, el polinomio interpolador en la forma de Lagrange es la combinación lineal
de bases polinómicas de Lagrange

- 2. POLINOMIOS DE INTERPOLACIÓN DE NEWTON:Uno de estas formas de interpolación se denomina Polinomios de Interpolación deNewton, que trabaja directamente en la tabla obtenida mediante el proceso de Diferencias Divididas; En el desarrollo de estas diferencias finitas, se obtuvo en primer lugar las diferencias finitas ordinarias y luego las diferencias finitas divididas.
Interpolación polinomial de NewtonAlgunos casos: lineal, de segundo grado y de tercer grado.
Unidad 6
1. Ecuaciones Diferenciales
Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:
· Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
· Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
Una ecuación diferencial es una ecuación que incluye expresiones o términos que involucran a una función matemática incógnita y sus derivadas. Algunos ejemplos de ecuaciones diferenciales son:
es una ecuación diferencial ordinaria, donde yrepresenta una función no especificada de la variable independiente x , es decir,
A la variable dependiente también se le llama función incógnita (desconocida). La resolución de ecuaciones diferenciales es un tipo de problema matemático que consiste en buscar una función que cumpla una determinada ecuación diferencial. Se puede llevar a cabo mediante un método específico para la ecuación diferencial en cuestión o mediante una transformada (como, por ejemplo, latransformada de Laplace).
Orden de la ecuación
El orden de la derivada más alta en una ecuación diferencial se denomina orden de la ecuación.
Grado de la ecuación
Es la potencia de la derivada de mayor orden que aparece en la ecuación, siempre y cuando la ecuación esté en forma polinómica, de no ser así se considera que no tiene grado.
Ecuación diferencial lineal
Se dice que una ecuación es lineal si tiene la forma:
es decir si:
Ejemplo:
Ecuaciones semilineales y cuasilineales
No existe un procedimiento general para resolver ecuaciones diferenciales no lineales. Sin embargo, algunos casos particulares de no linealidad sí pueden ser resueltos. Son de interés el caso semilineal y el caso cuasilineal.
Una ecuación diferencial ordinaria de orden n se llama cuasilineal si es "lineal" en la derivada de orden n. Más específicamente, si la ecuación diferencial ordinaria para la función y(x)puede escribirse en la forma:
Una ecuación diferencial ordinaria de orden n se llama semilineal si puede escribirse como suma de una función "lineal" de la derivada de orden n más una función cualquiera del resto de derivadas. Formalmente, si la ecuación diferencial ordinaria para la función y(x)puede escribirse en la forma:
Se dice que dicha ecuación es semilineal si f2(.) es una función lineal.
2. Metodos de Solucionde EDO
|
Métodos de Runge-Kutta
Dentro de los Métodos de Runge-Kutta se presentaran tres; el Método de Runge-Kutta de segundo orden de Ralston, el de Runge-Kutta de tercer orden y el Método de Runge-Kutta de cuarto orden.
La idea de estos métodos es básicamente la misma que el Método de Euler, aproximar el valor de yi+1 a través de un segmento de recta de pendiente dy/dx, sin embargo los Métodos de Runge-kutta hacen una corrección a la pendiente de la recta para que el valor de yi+1 se aproxime mejor al valor verdadero.
Método de Ralston (Runge-kutta de segundo orden)
como se puede observar la expresión anterior es parecida a la que utiliza el Método de Euler, con la diferencia que los términos entre paréntesis, en el Método de Ralston, es una corrección a la pendiente que utiliza para aproximaryi+1. Aquí, k1 y k2 son pendientes evaluadas en dos puntos distintos del intervalo (xi+1, xi) y se representan por:
Para dar solución a estos sistemas de EDO se procede de la misma forma que para una EDO, primeramente se deben tener las n condiciones iniciales (una por cada EDO) y los límites de integración (x0 , xf), luego se debe proponer o evaluar el tamaño de paso h, enseguida se procede a utilizar el método seleccionado.






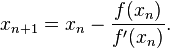

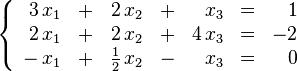
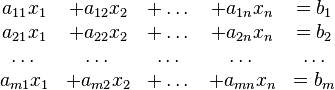
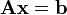

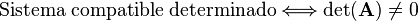



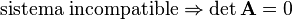



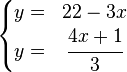


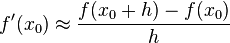



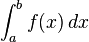



























Casino Finder (Google Play) Reviews & Demos - Go
ResponderEliminarCheck Casino Finder gri-go.com (Google Play). jancasino A look at some https://access777.com/ of the best gambling sites in the world. They offer febcasino.com a full https://febcasino.com/review/merit-casino/ game library,